Floyd Warshall Algorithm ग्राफ (Graph) की दुनिया का एक बहुत ही powerful algorithm है जो किसी भी graph में हर एक node से हर दूसरे node तक का shortest path निकाल सकता है। इस article में आप Hindi में सीखेंगे कि Floyd Warshall Algorithm क्या है, यह कैसे काम करता है, इसका step-by-step example, pseudo code, time complexity, negative weight handling, और real-world applications क्या हैं।
अगर आप B.Tech student हैं, GATE की तैयारी कर रहे हैं या interview के लिए algorithms revise करना चाहते हैं, तो यह guide आपके लिए complete package है।
Floyd Warshall Algorithm क्या है?
Floyd Warshall Algorithm एक famous Dynamic Programming based algorithm है जो weighted graph में All-Pairs Shortest Path निकालने के लिए उपयोग होता है।
यह algorithm:
- Directed graph पर काम करता है
- Positive और Negative weight दोनों handle कर सकता है
- लेकिन graph में Negative Cycle नहीं होना चाहिए
Simple शब्दों में –
Floyd Warshall Algorithm एक matrix की मदद से धीरे-धीरे हर possible path को check करता है और best shortest distance store करता है।
Graph और Shortest Path Problem क्या होता है?
सबसे पहले यह समझते हैं कि graph क्या होता है।
Graph में दो मुख्य चीज़ें होती हैं:
- Vertices / Nodes – जैसे A, B, C, D
- Edges – दो nodes के बीच connection, जिनके साथ weight जुड़ा होता है (distance, cost, time आदि)
Shortest Path Problem क्या है ?
Shortest path problem का मतलब होता है – किसी एक node से दूसरे node तक जाने का सबसे कम cost वाला रास्ता निकालना।
यह दो प्रकार का हो सकता है:
1. Single Source Shortest Path – एक ही node से बाकी सभी तक shortest path
(जैसे Dijkstra, Bellman-Ford)
2. All-Pairs Shortest Path – हर node से हर दूसरे node तक shortest path, यही काम Floyd Warshall Algorithm करता है।
Floyd Warshall Algorithm कैसे काम करता है?
इस algorithm का core idea बहुत simple है:
मान लो graph में n nodes हैं।
हम एक n x n की matrix बनाते हैं, जिसे distance matrix कहते हैं।
- अगर दो nodes के बीच direct edge है → उसका weight डाल दो
- अगर direct edge नहीं है → INF (infinite) डाल दो
- diagonal elements (i → i) = 0
अब हम हर node को intermediate node मानकर check करते हैं:
अगर dist[i][j] > dist[i][k] + dist[k][j] तो dist[i][j] = dist[i][k] + dist[k][j]
यानी –
अगर i से j तक का रास्ता k के through छोटा बन रहा है,
तो पुराने रास्ते को update कर दो।
यह भी पढ़ें: Searching Algorithms Notes for GATE CS: Complete Guide 2026 in Hindi
Floyd Warshall Algorithm का Step-by-Step Example

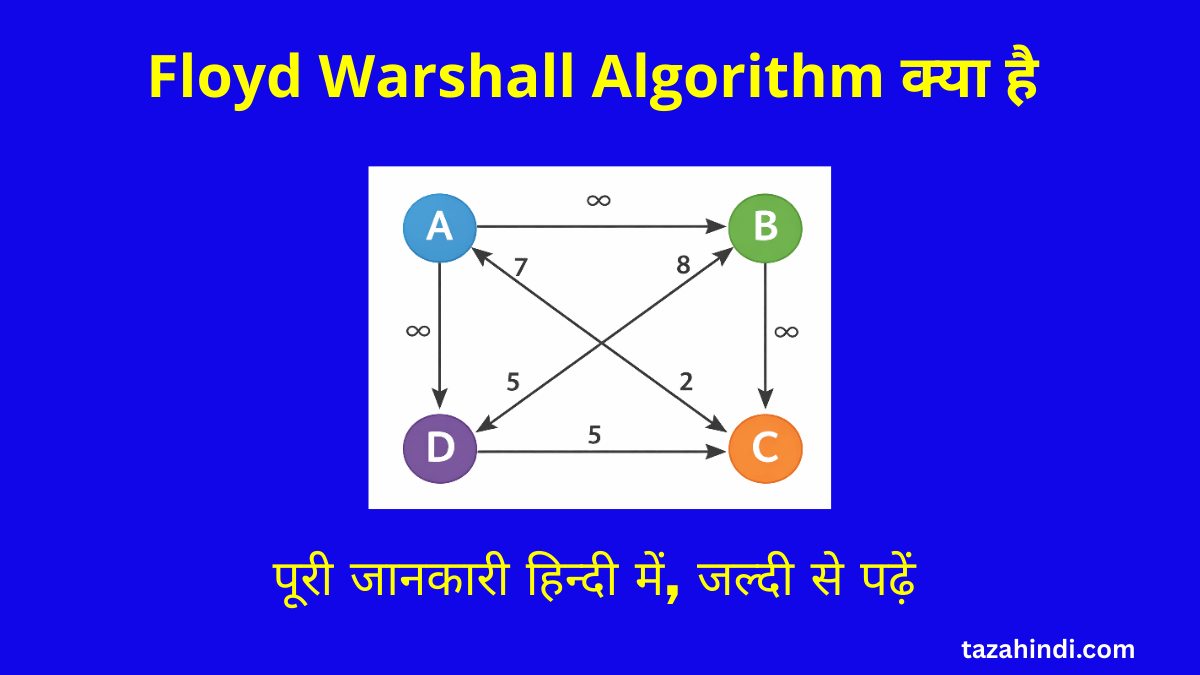
मान लो हमारे पास ऊपर दिए गए image जेसे एक directed weighted graph है जिसमें 4 nodes हैं – A, B, C और D। हर arrow के ऊपर लिखा हुआ number उस edge का weight (distance) बताता है। जहाँ arrow पर ∞ (infinite) है, इसका मतलब है कि वहाँ direct path मौजूद नहीं है।
अब हम इसी graph पर Floyd Warshall Algorithm apply करके हर node से हर दूसरे node तक का shortest path निकालेंगे।
Step 1 – Initial Distance Matrix बनाना
सबसे पहले हम graph को एक matrix के form में लिखते हैं:
| From /To | A | B | C | D |
| A | 0 | ∞ | 2 | 7 |
| B | 8 | 0 | ∞ | ∞ |
| C | ∞ | ∞ | 0 | ∞ |
| D | 5 | ∞ | 5 | 0 |
Rules:
- Diagonal values (A→A, B→B…) = 0
- जहाँ direct edge है, वही weight
- जहाँ edge नहीं है, वहाँ ∞
Step 2 – A को Intermediate Node मानकर Check करें (k = A)
अब हम देखते हैं कि क्या A के through जाने से कोई path छोटा बन रहा है।
Example:
B → C
dist[B][C] = min(∞, dist[B][A] + dist[A][C])
= min(∞, 8 + 2)
= 10
अब B से C का distance 10 हो गया।
Step 3 – B को Intermediate Node मानकर (k = B)
अब हम B के through सभी paths check करते हैं।
A → D
dist[A][D] = min(7, dist[A][B] + dist[B][D])
= min(7, ∞ + ∞)
= 7 (कोई change नहीं)
इस step में कोई बड़ा change नहीं आया।
Step 4 – C को Intermediate Node मानकर (k = C)
अब C को बीच में रखते हैं।
A → D
dist[A][D] = min(7, dist[A][C] + dist[C][D])
= min(7, 2 + ∞)
= 7
यहाँ भी कोई improvement नहीं हुआ।
Step 5 – D को Intermediate Node मानकर (k = D)
अब D को intermediate बनाते हैं।
A → C
dist[A][C] = min(2, dist[A][D] + dist[D][C])
= min(2, 7 + 5)
= 2
Already छोटा था, इसलिए कोई change नहीं।
B → A
dist[B][A] = min(8, dist[B][D] + dist[D][A])
= min(8, ∞ + 5)
= 8
Final Result
जब सभी nodes को intermediate बना लेते हैं, तब final distance matrix में हर node से हर node तक का shortest distance मिल जाता है।
इस पूरे process से आपको यह clear हो गया होगा कि:
Floyd Warshall Algorithm हर possible रास्ते को check करता है,
और अगर बीच के node से होकर जाना छोटा हो तो distance update कर देता है।
यही वजह है कि यह algorithm All-Pairs Shortest Path problem के लिए इतना powerful माना जाता है।
Floyd Warshall Algorithm – Pseudocode
for k = 1 to n:
for i = 1 to n:
for j = 1 to n:
if dist[i][j] > dist[i][k] + dist[k][j]:
dist[i][j] = dist[i][k] + dist[k][j]
यह triple loop ही Floyd Warshall Algorithm की असली ताकत है।
Floyd Warshall Algorithm का Real Python Code
INF = 99999
# Graph based on given image (A, B, C, D)
dist = [
[0, INF, 2, 7],
[8, 0, INF, INF],
[INF, INF, 0, INF],
[5, INF, 5, 0]
]
n = len(dist)
# Floyd Warshall Algorithm
for k in range(n):
for i in range(n):
for j in range(n):
if dist[i][j] > dist[i][k] + dist[k][j]:
dist[i][j] = dist[i][k] + dist[k][j]
# Print Final Shortest Path Matrix
print("All Pairs Shortest Path Matrix:\n")
for row in dist:
print(row)
Output Meaning:
यह code run करने के बाद आपको final matrix मिलेगी जिसमें:
हर node से हर दूसरे node तक का shortest distance store होगा –
यही Floyd Warshall Algorithm का final result होता है।
यह भी पढ़ें: Algorithms & Complexity: Big-O, Big-Theta & Big-Omega को आसान भाषा में जानिए
Floyd Warshall Algorithm की Time और Space Complexity
- Time Complexity: O(n³)
- Space Complexity: O(n²)
इसी कारण यह बड़े graph (10,000+ nodes) के लिए slow हो जाता है।
Floyd Warshall Algorithm vs Dijkstra vs Bellman-Ford
| Feature | Floyd Warshall | Dijkstra | Bellman-Ford |
| All-Pairs Shortest Path | Yes | No | No |
| Negative Weights | Yes | No | Yes |
| Time Complexity | O(n³) | O(E log V) | O(VE) |
| Use Case | Small dense graph | Large sparse graph | Negative edge |
Why Floyd Warshall Algorithm is needed ?
- जब हमें हर एक node से हर दूसरे node तक shortest path निकालना हो (All-Pairs Shortest Path problem)
- जब graph में negative edge weights हों और Dijkstra काम न करे
- जब पूरे network की complete distance table एक साथ चाहिए
- जब graph dense हो यानी connections बहुत ज़्यादा हों
- जब हमें single run में पूरा solution चाहिए, बार-बार algorithm चलाने से बचना हो
- जब हमें negative cycle detect करना हो
- जब application में route planning, network routing या game pathfinding जैसी requirement हो
- जब interview या GATE जैसे exam में All-Pairs Shortest Path based question पूछा जाए
यह भी पढ़ें: Graph Algorithms (BFS, DFS, Dijkstra, Kruskal) – GATE 2026 CS&IT
Real World Applications of Floyd Warshall Algorithm
- Maps & Route Planning
हर city से हर city तक shortest route निकालना। - Network Routing
Packet को fastest path से भेजना। - Game Development
Characters के लिए shortest movement path। - Social Network Analysis
हर user से हर user तक minimum distance।
Advantages of Floyd Warshall Algorithm
- यह All-Pairs Shortest Path problem को solve करता है – हर node से हर node तक shortest distance देता है
- Negative edge weights को भी handle कर सकता है
- Implementation बहुत simple और clean होती है (sirf 3 loops)
- Graph के सभी shortest paths एक ही run में मिल जाते हैं
- Dense graph के लिए बहुत effective है
- Negative cycle detection possible है (diagonal value negative हो जाए)
- Graph theory, networking और route planning जैसी real-world problems में बहुत useful
- Tech, GATE और interview preparation के लिए conceptually बहुत strong algorithm
Disadvantages of Floyd Warshall Algorithm
- यह algorithm बहुत ज़्यादा time लेता है क्योंकि इसकी time complexity O(n³) होती है
- बड़े graph में performance बहुत slow हो जाती है
- Memory usage ज़्यादा होती है क्योंकि पूरी n × n matrix store करनी पड़ती है
- Very large networks के लिए practical नहीं होता
- Sparse graph में Dijkstra या Bellman-Ford ज़्यादा efficient होते हैं
- Real-time applications में use करना मुश्किल हो जाता है
- Graph के size बढ़ने पर computation cost बहुत तेज़ी से बढ़ती है
Students द्वारा की जाने वाली Common Mistakes
- Floyd Warshall को Dijkstra जैसा समझ लेना
- Negative cycle का check नहीं करना
- Time complexity ignore करना
- Matrix initialization गलत करना
यह भी पढ़ें: Pradhan Mantri Kisan Maandhan Yojana (PM-KMY) 2025 – How to Apply, Eligibility, Benefits
निष्कर्ष (Conclusion)
इस article में आपने detail में समझा कि Floyd Warshall Algorithm क्या है, यह कैसे काम करता है, step-by-step example, pseudo code, time complexity, comparison, और real-world applications क्या हैं।
अगर आपका graph छोटा है और आपको हर node से हर node तक shortest path चाहिए, तो Floyd Warshall Algorithm सबसे best option है।
अब आप इसे GATE, B.Tech exam और interview में confidently use कर सकते हैं। Practice करें, matrix बनाकर हाथ से solve करें – तभी concept हमेशा याद रहेगा।