In computer science, trees play a vital role in data organization and manipulation. They provide efficient ways to store and retrieve information. In this article, I will explain you difference between Binary Tree and Binary Search Tree. Understanding these structures is crucial for programmers and developers as they serve different purposes and possess unique characteristics. Also explore the definitions, characteristics, advantages, uses and the disparities between Binary Tree and Binary Search Tree.
Importance of trees in computer science
Trees are hierarchical data structures widely used in computer science and programming. They offer efficient storage and retrieval mechanisms, making them indispensable in various algorithms and applications. Trees provide a way to represent relationships, hierarchies, and organized data, facilitating quick and optimized operations on large datasets.
What is Binary Tree?
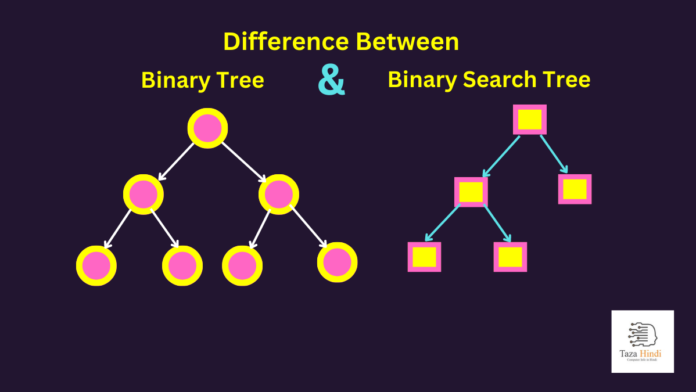
A Binary Tree is a type of tree structure in which each node can have at most two children, referred to as the left child and the right child. The nodes are connected through links called edges, forming a hierarchical structure. The Binary Tree allows for easy traversal, insertion, and deletion of nodes.
Also Read : What is Binary Arithmetic and uses of Binary Arithmetic in Computer
Characteristics of Binary Tree
- Each node in a Binary Tree can have at most two children.
- The left child is typically smaller or equal to the parent, while the right child is larger or equal.
- The order of insertion is crucial in maintaining the structure and properties of the Binary Tree.
Structure of binary trees
A Binary Tree comprises nodes connected through edges. Each node can have two pointers, one pointing to the left child and the other to the right child. The topmost node is called the root, and nodes at the lowest level, with no children, are called leaf nodes.
Also Read : Top 10 Web Development Frameworks for Building Websites
Properties of binary trees
- Height: The height of a Binary Tree is the number of edges on the longest path from the root to a leaf node.
- Depth: The depth of a node is the number of edges from the root to that particular node.
- Balanced vs. Unbalanced: A Binary Tree is considered balanced when the heights of its left and right subtrees differ by at most one. Otherwise, it is unbalanced.
Advantages of Binary Trees
- Efficient data storage: Binary Trees provide a compact and efficient way to store and organize data.
- Quick searching: Traversing a Binary Tree allows for efficient searching and retrieval of data.
- Easy implementation: Binary Trees are relatively simple to implement and manipulate, making them widely used in various applications.
Also Read : How to Convert String to Enum in C#: A Comprehensive Guide
Uses of Binary Trees
- File systems: Binary Trees are used to represent the hierarchical structure of file systems, enabling quick navigation and retrieval of files.
- Expression evaluation: Binary Trees can represent mathematical expressions, allowing for efficient evaluation and calculation.
What is Binary Search Tree?
A Binary Search Tree (BST) is a specific type of Binary Tree that follows a particular ordering property. In a Binary Search Tree, the left child of a node contains a value smaller than the parent, while the right child contains a value greater than or equal to the parent. This property enables efficient searching and retrieval of data.
Characteristics of Binary Search Tree
- Each node in a Binary Search Tree follows the ordering property: left child < parent < right child.
- The ordering property allows for quick search operations, making Binary Search Trees suitable for applications requiring efficient data retrieval.
Also Read : How to convert string to integer in C#
Structure of binary search trees
Similar to Binary Trees, Binary Search Trees consist of nodes connected through edges. However, in a Binary Search Tree, the nodes are ordered based on their values, following the rule that the left child is smaller than the parent, and the right child is greater than or equal to the parent.
Properties of binary search trees
In-order traversal: When performing an in-order traversal on a Binary Search Tree, the values of the nodes are visited in ascending order. 2. Unique values: Binary Search Trees do not allow duplicate values. Each node has a unique value.
Advantages of Binary Trees
- Efficient searching: The ordering property of Binary Search Trees allows for efficient search operations. The search process can be optimized by traversing only a portion of the tree.
- Quick insertion and deletion: Binary Search Trees provide efficient mechanisms for inserting and deleting nodes while maintaining the ordering property.
- Sorted data retrieval: In-order traversal of a Binary Search Tree yields data in sorted order, making it suitable for applications that require sorted data retrieval.
Also Read : How to Learn and Master Python Programming within one month
Uses of Binary Trees
- Dictionaries: Binary Search Trees are commonly used to implement dictionaries or symbol tables, where data is stored in key-value pairs.
- Database systems: Binary Search Trees are utilized in indexing and searching operations within database systems, enabling quick data retrieval.
Difference Between Binary Tree and Binary Search Tree
- Ordering Property: In a Binary Tree, there is no specific ordering property among the nodes. In contrast, a Binary Search Tree follows the ordering property, with each node’s value being greater than its left child and smaller than or equal to its right child.
- Search Efficiency: Binary Search Trees provide efficient search operations due to their ordering property. Binary Trees do not have this property, so searching involves traversing the entire tree.
- Data Retrieval: In a Binary Search Tree, an in-order traversal yields data in sorted order, which is not guaranteed in a Binary Tree.
- Usage: Binary Trees are suitable for general data storage and manipulation scenarios, while Binary Search Trees are ideal for applications that require efficient searching and sorted data retrieval.
Also Read : How to Learn Data Types in TypeScript
Note: If you would like to learn through watching video, then you can watch the video given below, I hope your doubt will be fully clear after watching complete video.
Conclusion
Binary Trees and Binary Search Trees are important tree structures used in computer science and programming. Understanding their characteristics, properties, advantages, and differences is crucial for selecting the appropriate structure for specific applications. Binary Trees provide a flexible way to store and organize data, while Binary Search Trees offer efficient searching and sorted data retrieval capabilities. By grasping the distinctions between these two structures, programmers and developers can make informed decisions regarding their implementation in various algorithms and applications.
FAQs
-
Can a Binary Tree be transformed into a Binary Search Tree?
Yes, it is possible to convert a Binary Tree into a Binary Search Tree by rearranging the nodes and ensuring that the ordering property is satisfied. However, this transformation may require additional operations and may not always be practical or efficient.
-
Can a Binary Tree be used for efficient searching?
No, a Binary Tree does not possess any specific ordering property, making searching less efficient compared to a Binary Search Tree. Traversing a Binary Tree involves checking every node, resulting in a time complexity of O(n), where n is the number of nodes in the tree.
-
Can a Binary Search Tree contain duplicate values?
In a standard Binary Search Tree, duplicate values are not allowed. Each node must have a unique value. However, variations of Binary Search Trees, such as Binary Multi-Search Trees, can be designed to accommodate duplicate values.
-
Are all Binary Search Trees balanced?
No, not all Binary Search Trees are balanced. A Binary Search Tree can become unbalanced if nodes are inserted or deleted in a specific order. Balanced Binary Search Trees, such as AVL trees or Red-Black trees, are designed to maintain a balanced structure, ensuring efficient operations in all cases.
-
Can a Binary Search Tree be unbalanced?
Yes, a Binary Search Tree can become unbalanced if nodes are inserted or deleted in a way that violates the ordering property. An unbalanced Binary Search Tree may lead to inefficient search operations, as the tree’s height increases, impacting its performance.